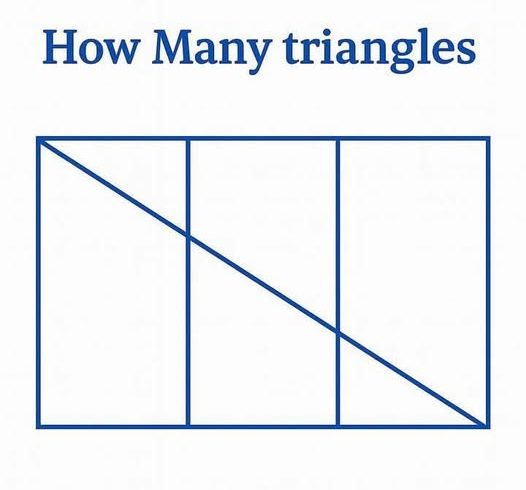
In this image, the question is: “How many triangles are there?” At first glance, it looks like a simple rectangle divided by lines, but careful observation reveals multiple overlapping and nested triangles.
Step-by-step Breakdown:
The large rectangle is divided vertically into 4 equal sections and a diagonal line runs from the top-left corner to the bottom-right corner, cutting through each vertical section.
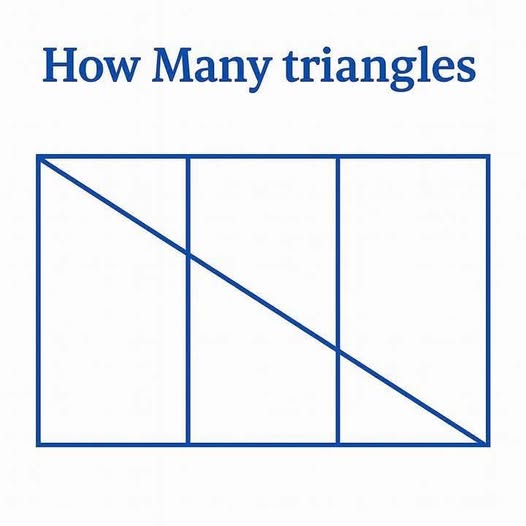
Let’s count the triangles section by section:
1. First Section (far left):
The diagonal cuts this square into 2 triangles.
2. Second Section:
The diagonal creates 2 more triangles here.
3. Third Section:
Again, 2 triangles formed by the diagonal.
4. Fourth Section (far right):
The diagonal again forms 2 triangles.
That gives us 2 triangles × 4 sections = 8 small triangles.
Now, consider larger combinations:
5. Larger triangles formed across sections:
– One triangle spans the first and second section.
– One triangle spans second and third section.
– One spans third and fourth section.
– One triangle spans entire top half of the rectangle.
– One triangle spans entire bottom half.
– One large triangle covering the whole diagonal shape.
These larger combinations add 6 more triangles.
✅ Total = 8 (small) + 6 (larger) = 14 triangles
Conclusion:
The puzzle contains a total of 14 triangles, formed by cleverly combining small and large sections. This visual riddle tests not only attention to detail but also spatial awareness and geometric understanding.






